Untersuchung einer oder mehrerer Zeitreihe(n) zur Aufdeckung von Gesetzmäßigkeiten, die zur Erklärung oder Prognose (siehe Prognoserechnung) durch Anpassung eines Modells an die Daten dienen können.
Als Zeitreihe {xt} wird eine Menge von Beobachtungen an einem statistischen Merkmal X in zeitlicher Abfolge bezeichnet. Der Zeitbezug kann punktuell wie z. B beim stündlich erfassten Strompreis eines Energiegroßhändlers oder intervallbezogen wie z. B. beim jährlich abgelesenen Elektroenergieverbrauch eines Haushalts sein.
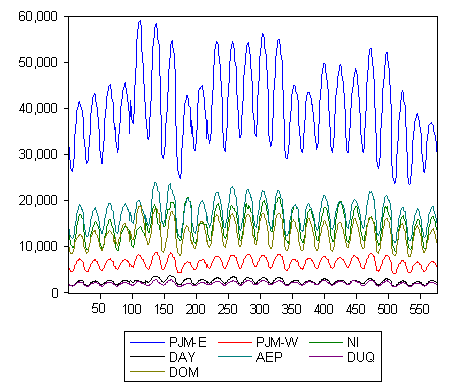
Die Analyse einer Zeitreihe soll dynamische Gesetzmäßigkeiten beim Verlauf eines Merkmals oder der Wechselwirkung zwischen mehreren Merkmalen aufdecken. Sie ist der Regressionsanalyse verwandt, wenn die Zeit als Regressor und das zu untersuchende Merkmal X als Regressand gedeutet werden.
Die Methoden der Zeitreihenanalyse lassen sich nach deterministischen oder stochastischen, univariaten oder multivariaten Ansätzen unterscheiden. Zu jedem dieser Ansätze gehören Modellklassen und entsprechende Techniken zur Strukturspezifikation.
Ein deterministischer Ansatz beschreibt die Veränderungen im Mittel (Trend), mögliche zyklische Schwankungen, jährige Saisonschwankungen oder auch Kalendereffekte mit Hilfe von Funktionen, die meist additiv als Komponentenmodell in einer Gleichung überlagert werden (Dekomposition). Mit Hilfe von gleitenden Durchschnitten oder gleitenden Medianen lassen sich einzelne Komponenten aus dem Ansatz heraus filtern (Glättung). Bei einer Kalender- und Saisonbereinigung werden entsprechenden Komponenten heraus gerechnet, um die Trendentwicklung z. B. bei Arbeitsmarktdaten besser erkennen zu können. Ein einfaches Kriterium für die Wahl eines den Daten adäquaten Komponentenmodelles enthält die Methode der Kleinsten Quadrate.
Ein stochastischer Ansatz fasst die Daten als Realisierung eines oder mehrerer adäquater Zufallsprozesse auf und untersucht deren Gesetzmäßigkeiten. Vor der eigentlichen Modellierung sind mittels Spektralanalyse versteckte Periodizitäten aufzudecken [Schlittgen 2001, S. 353 ff.]. Mit Hilfe von Einheitswurzeltests wird auf Trendstationarität geprüft und für den Fall einer zeitabhängigen Varianz eine geeignete Box-Cox-Transformation vorgenommen.
Lassen sich Trend-, Saison- und Kalendereffekte durch Differenzenbildung entfernen, kann die verbleibende Restkomponente einer Autokorrelationsanalyse unterzogen werden, die Aufschluss über typische Reaktionen auf Zufallsschocks wie z. B. Witterungs- und Preisturbulenzen geben kann. Häufig verwendete, parametersparsame Modellprozesse sind vom Typ ARIMA (Autoregressive Integrated Moving Average) und bestehen aus einem autoregressiven Anteil mit gewichteten zeitverzögerten Beobachtungen und einem Gleitmittelanteil mit gewichteten zeitverzögerten Schocks. Zur Spezifikation der Differenzengleichung wird meistens die Box-Jenkins-Technik [Götze 2010, S. 199] angewendet. Die Schätzung der Parameter erfolgt mit Hilfe von Gradienten Verfahren.
Um vorgeschaltete Transformationen der Daten zu vermeiden, werden mitunter Mehrgleichungsmodelle mit separaten Modellprozessen für die Niveau-, die Trend- und die Saisondynamik angesetzt. Die einzelnen Modellprozesse können wie z. B. bei UCM (Unobserved Components Models) nahezu parameterfrei strukturiert sein, wodurch sich der Identifikationsaufwand erheblich verringert [Brockwell 2002, S. 259 ff.]. Erweiterungen dieses Ansatzes durch deterministische Komponenten wie Kalendereffekte und Interventionsterme, aber auch durch autoregressive Terme sind möglich.
Im Falle zeitvariabler Volatilität kann über die eigentliche Beobachtungsgleichung hinaus eine Varianzgleichung vom Typ GARCH (General Autoregressive Heteroskedasticity) mit einbeziehen werden, die zeitverzögerte gewichtete Varianzen und quadrierte Schocks enthält [Hill 2008, S. 363 ff.]. Auf diese Weise lassen sich dynamische Vertrauensintervalle für Einschrittprognosen konstruieren.
Ein multivariater stochastischer Ansatz dient zur Untersuchung von mutmaßlichen Wechselwirkungen zwischen mehreren Modelprozessen, z. B. zwischen der Tagesdurchschnittstemperatur und dem Energieverbrauch eines Kühlhauses. Dazu dienen Kreuzspektral- und Kreuzkorrelationsanalysen. Weit verbreitet sind Modellgleichungssysteme vom Typ VAR (Vektorautoregression), die eine simultane Beschreibung von Zeitreihenbündeln ermöglichen, allerdings eine Vielzahl kaum noch interpretierbarer Modellparameter enthalten [Hill 2008, S. 346 ff.].
Im Fall mehrerer nichtstationärer Modellprozesse kann es sinnvoll sein, Linearkombinationen on Zeitreihen zu untersuchen, um das Zusammenspiel von langfristiger und kurzfristiger Dynamik abzubilden (Kointegration). Differenzengleichungen beschreiben die kurzfristigen Veränderungen jeder einzelnen Variablen (Fehlerkorrekturgleichungen) und schließen eine Reg-ressionsbeziehung zwischen den Variablen ein, die für das langfristige Gleichgewicht steht [Hill 2008, S. 339].
Bei einer Modellierung von Zeitreihen garantieren vor allem Normalprozesse optimale statistische Parameterschätzungen. Mit Hilfe einer logarithmischen Datentransformation lässt sich oftmals die Schiefe erheblich reduzieren und die Normalverteilungsannahme unterstützen. Bei einer Kerndichteschätzung wird anstelle einer angenommenen Wahrscheinlichkeitsverteilung mit der empirischen Häufigkeitsverteilung gearbeitet. Dabei sind zwei Annahmen über die Gewichtsfunktion (Kerndichtefunktion) und den Glättungsparameter (Bandbreite) zu treffen. Für den weit verbreiteten Gaußkern lässt sich eine optimale Bandbreite bestimmen [Hildebrandt 2009, S. 76 ff.].
Literatur
Brockwell, P. J.; Davis, R. A.: Introduction to Time Series and Forecasting. 2. Auflage, Springer, 2002.
Götze, W.: Techniken des Business Forecasting. Oldenbourg, 2. Auflage 2010.
Hildebrandt, J.: Nichtparametrische integrierte Rendite- und Risikoprognosen im Asset Management mit Hilfe von Prädiktorselektionsverfahren, Göttingen, Cuvillier, 2009 (Diss.).
Hill, R. Carter, William E. Griffiths, Guay C. Lim: Principles of Econometrics. 3rd Edition, John Wiley & Sons Inc. 2008.
Schlittgen, R.; Streitberg, B. H. J.: Zeitreihenanalyse. 9. Auflage, Oldenbourg, 2001