Prognoseverfahren

Prognoseverfahren unterschiedlicher Reichweite sind Komponenten von betrieblichen Anwendungssystemen, mit denen kurzfristig disponiert oder mittelfristig geplant wird.

Systematisierung

Prognoseverfahren werden häufig nach der ihnen zugrunde liegenden Methodik unterschieden. Wir kennen Verfahren, die auf die einfache Extrapolation von Zeitreihen mithilfe gleitender Durchschnitte, ggf. unter Modellierung von Saisonprofilen, zurückgeführt werden können. Unter dem Begriff Komponentenmodelle werden die Modelle von Holt-Winters, Methoden der Exponentiellen Glättung, aber z. B. auch bayesianische Strukturkomponentenmodelle subsumiert. Weitere Vorhersageverfahren liefert die klassische Regressionsanalyse. Aus der Zeitreihenanalyse sind wiederum Box-Jenkins-Modelle oder auch ARIMA- oder SARIMA-Modelle (Saisonale Autoregressive Integrierte Moving-Average-Modelle) bekannt. Bei der Modellierung von Finanzmarktzeitreihen spielen hingegen Volatilitäten eine wichtige Rolle, hier nehmen ARCH- bzw. GARCH-Modelle (verallgemeinerte autoregressive, bedingt heteroskedastische Modelle) und viele Erweiterungen eine dominante Stellung ein. Der statistische Methodenkasten bietet nahezu beliebig komplexe Verfahren. Ferner können Methoden der Mustererkennung aus dem Bereich der Künstlichen Intelligenz zur Prognoserechnung herangezogen werden. Doch nicht die formale Komplexität des Modells ist entscheidend, sondern seine Leistungsfähigkeit im alltäglichen Betrieb und seine Verständlichkeit für den Nutzer bzw. Planer sind es.

Anwendungsgebiete in der Wirtschaftsinformatik

Prognosen spielen vor allem in Systemen eine Rolle, mit denen kurzfristige Dispositionen möglichst vollautomatisch durchgeführt werden sollen. Dies sind Beschaffungsprozesse bei B- und C-Teilen, die Vorhersage von Absatzmengen oder von Zahlungsein- und -ausgängen im Rahmen der Liquiditätsdisposition. Primäres Ziel ist es nicht, die Vorhersagegenauigkeit zu erhöhen; vielmehr soll vermieden werden, dass automatische Massenprozesse durch aufwändige personelle Interventionen unterbrochen werden müssen. Für Zwecke der mittelfristigen Planung eignen sich Verfahren, bei denen der Bedarf an Ersatzteilen für die ausgelieferten Erzeugnisse abzuschätzen oder aus den Beobachtungen in der Frühphase der Markteinführung eines neuen Produkts (vor allem mit Hilfe von Panels) auf den endgültigen Produkterfolg zu schließen ist. Für die strategische Planung sind meist sehr individuelle Vorhersagemethoden zum Bedarf an Produktionsfaktoren (Personal in bestimmten Qualifikationsgruppen, Produktions- und Logistikkapazitäten) nützlich. Sie dienen u. a. als Grundlage für Investitions-/Desinvestitionsentscheidungen sowie für Anpassungen des Mitarbeiterbestands in beide Richtungen.

Verfahrensklasse Exponentielles Glätten als Grundbaustein

Die von der Menge der Aufrufe durch betriebliche Anwendungssysteme her weitaus am meisten genutzte Methodenklasse dürfte das Exponentielle Glätten sein [Schr12]. Fast alle Standardsoftwarepakete der Materialwirtschaft z. B. nutzen diese Methoden zur kurzfristigen Zeitreihenprognose des Lagerabgangs und damit des Nachbevorratungsbedarfs einzelner Artikel in Handel und Industrie. Abbildung 1 zeigt Modelle für Zeitreihen ohne Periodizität, wobei jeweils danach unterteilt wird, ob der zugrunde liegende Prozess über der Zeit konstant (A), eine linear wachsende Funktion der Zeit (B) oder eine nicht-linear wachsende Funktion der Zeit (C) ist. Die ausgezogenen Linien stellen den Prozess dar, der durch das Modell beschrieben werden soll, während die Abstände der Beobachtungswerte von diesen Linien das Ergebnis der nicht vorhersagbaren Zufallsabweichungen sind. In Abbildung 2 überlagern periodische Schwankungen den Grundwert additiv. Erlebt ein Erzeugnis beispielsweise zu Beginn des Frühjahrs ein Absatzplus, zu Beginn der Urlaubsperiode aber jeweils einen Absatzeinbruch, so wären etwa im April positive und im Juli negative Summanden zu berücksichtigen. Beim multiplikativen Verfahren werden die ursprünglichen Prognosewerte mit Saisonfaktoren multipliziert, z. B. im April mit 1,2 und im Juli mit 0,8. Die multiplikative Methode bringt den Nachteil mit sich, dass im ersten Schritt errechnete Prognose-Ist-Abweichungen durch die Multiplikation besonders verstärkt werden.

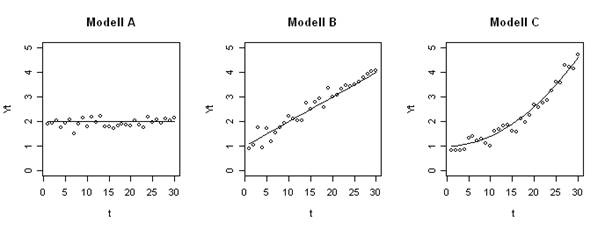
Abbildung 1: Modelle für Zeitreihen ohne Periodizität/Saison

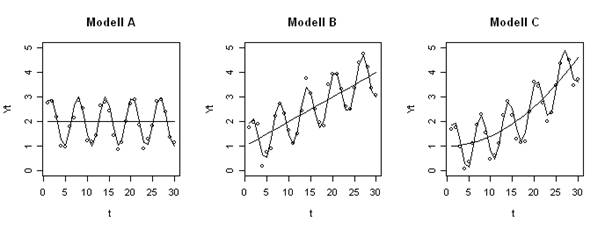
Abbildung 2: Modelle für Zeitreihen, bei denen periodische/saisonale Schwankungen den Grundwert additiv überlagern

Betrachten wir beispielsweise die Prognose des Lagerabgangs aufgrund des in der Vergangenheit beobachteten Verbrauchs mithilfe einer Zeitreihenprognose, z. B. mit der Exponentiellen Glättung: Das einfache Exponentielle Glätten erster Ordnung geschieht nach der Formel

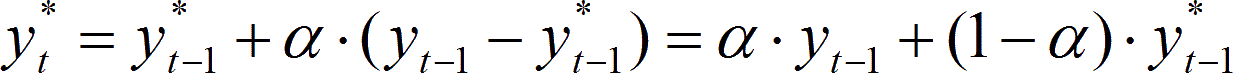  für t = 1, 2, …, T.

Darin bedeuten
    : Vorhergesagter Bedarf für die Periode

t
  : Vorhergesagter Bedarf für die Periode

t-1

: Tatsächlicher Bedarf in der Periode

t-1
     : Glättungsparameter (0 ≤

α ≤ 1 )

Verbal dargestellt errechnet sich also der neue Prognosewert aus dem alten Prognosewert plus einem Bruchteil α der zuletzt beobachteten Prognoseabweichung. Mit dem Parameter α kann der Systembetreiber zum Ausdruck bringen, ob das Modell sich sensibel an die neueste Entwicklung anpassen soll (die jüngsten Beobachtungen werden stark gewichtet) oder ob es ihm mehr auf einen “ruhigen” Verlauf ankommt (der letzte Prognosewert geht mit relativ starkem Gewicht ein). Der ruhigere Verlauf und damit die Wahl eines kleinen α sind von Vorteil, wenn eher zufällige Nachfragespitzen “herausgeglättet” werden sollen. Ein Nachteil ist, dass das Verfahren viele Perioden braucht, um sich auf eine bleibende Niveauänderung einzustellen.

Verläuft das Prognoseobjekt über der Zeit trendförmig, z. B. weil sich ein neu eingeführtes Produkt auf dem Markt rasch etabliert oder ein älteres immer weniger gekauft wird, so kann das konstante Modell um diesen Trend korrigiert werden, oder man wählt das Exponentielle Glätten zweiter Ordnung. Der vorhergesagte Bedarf für die Periode t errechnet sich dann nach der Formel:

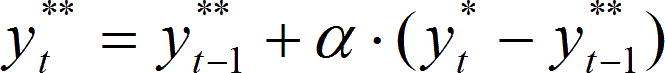  für t = 1, 2, …, T

Die Doppelsterne bezeichnen Werte zweiter Ordnung.

In dieser Beziehung spielt der wie oben ermittelte Glättungswert erster Ordnung jene Rolle, die die beobachteten Lagerabgänge in der Formel zur Berechnung des Glättungswerts erster Ordnung übernehmen. In der Gleichung kommen die letzten Beobachtungswerte nicht mehr vor; vielmehr treten an deren Stelle die Ergebnisse der Berechnung des Glättungswerts erster Ordnung (“Glättung der Glättung”). Man kann diesen Gedankengang fortführen und gelangt so zu Glättungsverfahren noch höherer Ordnung. In der Praxis haben sich diese jedoch nicht durchgesetzt, weil sie zum einen nur schwer zu erklären sind und zum anderen oft “überreagieren”.

Zur nicht-parametrischen Statistik

Im Gegensatz zur klassischen parametrischen Statistik, in der etwa die Parameter von explizit formulierten Regressionsmodellen aus den Daten geschätzt und dann für Prognosezwecke in die Modellgleichung eingesetzt werden, erlauben z. B. “Classification and Regression Trees” (CART) eine flexible und doch sparsame nicht-parametrische Charakterisierung von bedingten Verteilungen und damit auch von bedingten Erwartungswerten, welche für Prognosezwecke gut geeignet sind. Insbesondere die Fähigkeit nicht-lineare Zusammenhänge ohne explizite Modellierung abzubilden, machen CART-Modelle zu einer Bereicherung für Standard-Vorhersagewerkzeuge, die auf linearen autoregressiven Prozessen basieren [HaTF08].

Ausgewählte spezielle Verfahren in der Wirtschaftsinformatik

Liquiditätsprognosen basieren häufig auf dem Exponentiellen Glätten von Zeitspannen (Auftrag, Durchlaufzeit, Transport zum Kunden, vom Kunden in Anspruch genommene Frist bis zur Bezahlung).

Den Bedarf an Ersatzteilen leiten Anwendungssysteme oft nach Art von Verweilzeitprognosen aus dem Verkauf der Fertigerzeugnisse (z. B. PKW) in früheren Perioden und der mittels Exponentiellem Glätten fortgeschriebenen Lebensdauer der Komponenten (z. B. Bremsscheiben) ab.

Vorhersagen des Lebenszyklus von Produkten gründen hingegen meist auf der Annahme, dass sich ein Erzeugnis auf einer logistischen Kurve oder einer Gompertzfunktion einem Sättigungswert entgegen bewegt. Die Prognose des gesamten Zyklus mit befriedigender Genauigkeit ist oft nicht möglich. Eher ist unter der Annahme eines Verlaufs, den das System nach Eintreffen neuer Daten justiert (adaptive Prognose), vorherzusagen, welchen Zuwachs an akkumuliertem Absatz ein Produkt im nächsten Zeitintervall (z. B. Quartal) verzeichnen wird. In der Startphase helfen Methoden vom Parfitt-Collins-Typ: Das System zieht Schlüsse aus Paneldaten, und zwar sowohl was die Erstkäufe des neuen Erzeugnisses angeht als auch was die Zahl der Kunden betrifft, die zum zweiten, dritten, … Mal kaufen, also aus der Wiederholkaufrate.

Zur Planung und Disposition in Liefernetzen (“Supply Chain Management”) hat man das “Collaborative Planning, Forecasting and Replenishment”, CPFR, entwickelt [MeZG12]. Die teilnehmenden Betriebe stimmen in normierten Prozeduren ihre Daten (z. B. Zeitreihen des bisherigen Absatzes, Kapazitätsrestriktionen) und/oder ihre Prognoseverfahren und -ergebnisse aufeinander ab, um so u. a. ihre Absatz-, Beschaffungs-, Lager-, Produktions- und Versandplanung auf eine möglichst solide Grundlage zu stellen.

Künstliche Neuronale Netze (KNN) und Maschinelles Lernen

Künstliche Neuronale Netze sind Methoden, die die Abläufe im Gehirn von Lebewesen nachahmen. Es wurden verschiedene Erscheinungsformen entwickelt, u.a. was das Lernen (Trainieren) der Netze an großen Datenbeständen betrifft (vgl. Neuronales Netz). KNN sind eine besonders wichtige Methodengruppe in der sogenannten Künstlichen Intelligenz.

Die Methoden basieren darauf, dass Muster verglichen werden: Wurde in der Vergangenheit ein Muster MV entdeckt, in dessen Folge in der Vergangenheit häufig ein bestimmtes Ereignis EV eintrat, so nimmt man beim Auftreten des gleichen Musters in der Gegenwart (MG = MV) an, dass ihm in der Zukunft das Ereignis EZ folgen wird, wobei EZ= EV.
Zwei Beispiele aus dem Vertrieb:
Das Vertriebsanalysesystem eines Telekommunikationsunternehmens erkennt, dass eine Anzahl von Kunden immer die Verlängerung ihres über zwei Jahre laufenden Vertrags mit dem Neuerwerb eines modernen Mobiltelefons verbindet, dessen Erstverkauf nicht länger als sechs Monate zurückliegt. Summiert über alle Kunden mit dieser „Deskriptorenkombination“ kann das Unternehmen abschätzen, welche Kunden man verlieren könnte, wenn nicht rechtzeitig vor dem Vertragsablauf ein geeignetes Nachfolgeprodukt bereitsteht. Es erwägt zusammen mit einem Hersteller von Mobiltelefonen eine Angebotsaktion.
Innerhalb einer Absatzprognose, die auch mit Vorhersagen des Bedarfs an Vorprodukten verbunden ist, erarbeitet ein KNN-System Muster, wie nach Menge und Zeitverlauf der Verkauf eines Unternehmens leidet, wenn ein direkter Konkurrent kurzfristig eine Rabattaktion durchführt.
Ein Beispiel aus der Fertigung:
In einem Automobilwerk werden bei geformten Karosserieblechen noch vor der Lackierung mit Hilfe mehrerer Sensoren kleine Risse an der Oberfläche gemeldet. Ein System erkennt, dass diese Risse unter weiteren technischen Bedingungen, z. B. wenn diese Unregelmäßigkeiten an einer Biegung des Bleches vorkommen, später mit beachtlicher Wahrscheinlichkeit zu kleinen Fehlern im Lack führen werden. Normalerweise entdeckt man diese Mängel erst bei der Qualitätskontrolle nach der Endmontage. Dann entstehen für die Behebung sehr hohe Kosten. Daher prognostiziert das System rechtzeitig das Risiko und empfiehlt, solche Bleche sofort nach dem Biegen auszusteuern [Sche17].
In engem Zusammenhang mit KNN steht das Maschinelle Lernen [GoBC16]: Es bleibt nicht bei einmaligen Analysen der Zusammenhänge zwischen Muster, wahrscheinlichen Folgewirkungen und einschlägigen Prognosen; vielmehr werden die Analysen in engen Abständen wiederholt und die Muster sowie deren Konsequenzen überprüft und verfeinert.

Predictive Analytics (ein deutscher Begriff hat sich noch nicht ausgeprägt) kombiniert moderne Verfahren der Auswertung von großen Datenvorräten, vor allem Data Mining, maschinelles Lernen auf der Grundlage der Künstlichen Intelligenz und gewisse statistische Methoden wie die Clusteranalyse mit klassischen Prognoseverfahren. Viele Definitionen verknüpfen die Beschreibung der Predictive Analytics direkt mit einem speziellen Anwendungsgebiet [FeKB12]. Beispielsweise wird unter Berücksichtigung vorhergesagter Entwicklungen das dann zu erwartende Verhalten bestimmter Verbrauchergruppen in Massenmärkten analysiert und zu typischen Mustern verdichtet. Eine bekannte Verfahrensgruppe sind Empfehlungssysteme („Recommender Systems“): Ein neuer Fall wird einem Muster bzw. Cluster zugeordnet. Das Verhalten von Verbrauchern in diesem Cluster ist bekannt. Der bisher unbekannte neue Mensch wird so behandelt, als ob er Element der gleichen Gruppe sei. Beispielsweise habe ein PKW-Hersteller herausgefunden, dass sich Liebhaber neuer Technik („Technik-Freaks“) sofort mit Innovationen befassen und hierfür auch Opfer bringen (Zahlung hoher Preise, Inkaufnahme von Umstellungs- und Lernaufwand, Toleranz gegenüber „Kinderkrankheiten“). Bringt der Hersteller eine neue Technik, so umwirbt er zunächst vor allem diejenigen Kunden, die seine Systeme in die Kategorie „Technik-Freaks“ eingruppiert hatten, weil eine überdurchschnittliche Prognose gegeben ist, dass der neue Abnehmer kauft.

Ein Einsatzfeld, von dem man sich weiterhin viel verspricht, ist die vorbeugende Wartung. Es werden zu überwachende Merkmale eines technischen Systems definiert. Bei einem Flugzeugtriebwerk könnten das Stand und Veränderung von Temperatur, Druck, Geräusche und Schwingungen sein, dies bei unterschiedlichen Umgebungsbedingungen wie Start, Horizontalflug, Turbulenzen und/oder Landung. Im einfachsten Fall überwacht ein System die einzelnen Größen für sich und beachtet Warnschwellen, die die Vorhersage erlauben, dass bald ein Defekt eintreten könnte. Angestrebt wird jedoch, bestimmten Kombinationen zu identifizieren, die Eingriffe geraten sein lassen, etwa Druckabfall bei gleichzeitig zunehmenden Amplituden von Schwingungen oder ungewöhnlicher Temperaturerhöhung. Die großen Fortschritte beim Preis-Leistungs-Verhältnis der Sensoren fördern die automatische Identifikation solcher Konstellationen. Die Herausforderung auf Seiten der Technik liegt darin, aus den Mustern (Symptomatik) auf die Ursachen zu schließen (Diagnose), Vorbeuge- bzw. Reparaturmaßnahmen damit zu verknüpfen (Therapie), sodass „Therapieprognosen“ gewonnen werden können, die wiederum möglichst automatisch, etwa mit Regressionsrechnungen, zu überwachen sind. Im Idealfall sind die skizzierten Verknüpfungen automatisch zu finden (Methodengruppe „Maschinelles Lernen“ vgl. auch das Stichwort  Neuronales Netz).

In der Finanzwirtschaft ist in besonderem Maße das sog. Herdenverhalten bekannt. So drohen z. B. beim Auftauchen beunruhigender Gerüchte Bankpaniken (ein großer Teil der Kundschaft hebt kurzfristig die Ersparnisse ab). Es gibt – freilich am Anfang stehende – Überlegungen, durch maschinelle Sprachanalyse in der Kommunikation in Sozialen Netzen Anzeichen zu finden, dass eine Massenreaktion entstehen könnte, etwa wenn sich bestimmte Wörter („Deskriptoren“) oder Wortverbindungen (hier: z. B. Geld abheben, Bankautomat, Beschlagnahme, Schließung von Banken, Kopfkissen, „Bankfeiertage“) plötzlich häufen.

Der Prognoseprozess

Einen stark personell eingerichteten, parametrierten und überwachten Prognoseprozess kann man sich aus den folgenden sechs Phasen zusammengesetzt vorstellen:

1. Darstellung der Zeitreihen

2. Wahl des Verfahrens

3. Parametrierung des Verfahrens

4. Prognose

5. Kontrolle der Vorhersage-Ist-Abweichungen mit Hilfe von statistischen Abweichungsmaßen

6. Korrektur durch Umregulierung der Parameter oder Wahl eines anderen Verfahrens

In leistungsfähigen Standardsoftware-Systemen, insbesondere zur Materialwirtschaft, aber ebenso zu anderen Feldern, wie z. B. der Liquiditätsdisposition, finden sich auch Mechanismen zur stärkeren Automation des Prozesses. Insbesondere versuchen die Systeme auf der Grundlage ausgewählter Prognoseobjekte und deren Zeitreihen, durch Simulation herauszufinden, welches Verfahren mit welcher Parameterkonfiguration die geringsten Prognose-Ist-Abweichungen erreicht. Darüber hinaus können, z. B. auf der Grundlage eines Regelwerks, in Abhängigkeit von der Qualität der Vorhersage auch automatische Adaptionen vorgenommen werden. Registriert das System z. B., dass die Vorhersagewerte oft einem Trend nicht folgen können, so schaltet es vom Exponentiellen Glätten erster Ordnung auf das Glätten zweiter Ordnung um.

Bei Erzeugnissen mit ausgeprägtem Lebenszyklus mag es sich zudem empfehlen, die Vorhersagen in der Frühphase, in der es noch an statistischen Daten mangelt, personell abzugeben. Das System kann aufgrund eines entsprechenden Tests autonom feststellen, wann ihm die Datengrundlage für eine automatische Prognose ausreicht, und dies dem Sachbearbeiter signalisieren. Im Auslaufstadium wird sich das System umgekehrt von einem bestimmten Punkt an außer Stande erklären, weiter auf der Grundlage seines Algorithmus Prognosen abzugeben, weil die Absatzzahlen stark zurückgehen und infolgedessen die statistische Grundlage wegfällt.

---

Literatur

[FeKB12] Felden, C., Koschtial, C. und Buder, J. (2012). Predictive Analytics in der Strategischen Anlagenwirtschaft, in: Mertens, P., Rässler, S. (Hrsg.) (2012). Prognoserechnung. 7. wesentlich überarbeitete und erweiterte Auflage, Springer, Heidelberg, S. 519-537.

[GoBC16] Goodfellow, I., Bengio, Y., Courville, A. (2016). Deep Learning (Adaptive Computation and Machine Learning) MIT Press, Cambridge.

[HaTF08] Hastie, T., Tibshirani, R., Friedman, J. (2008). The Elements of Statistical Learning. Data Mining, Inference, and Prediction, 2. Auflage, Springer, Heidelberg.

[MeRä12] Mertens, P., Rässler, S. (Hrsg.) (2012). Prognoserechnung. 7. wesentlich überarbeitete und erweiterte Auflage, Springer, Heidelberg.

[MeZG12] Mertens, P., Zeller, A.-J. und Große-Wilde, J. (2012). Kooperative Vorhersage in Unternehmensnetzwerken, in: Mertens, P., Rässler, S. (Hrsg.) (2012). Prognoserechnung. 7. wesentlich überarbeitete und erweiterte Auflage, Springer, Heidelberg, S. 621-637.

[Sche17] Scheer, A.-W. (2017). Performancesteigerung durch Automatisierung von Geschäftsprozessen, AWS-Institut, Saarbrücken.

[Schr12] Schröder, M. (2012). Einführung in die kurzfristige Zeitreihenprognose und Vergleich der einzelnen Verfahren, in: Mertens, P., Rässler, S. (Hrsg.) (2012). Prognoserechnung. 7. wesentlich überarbeitete und erweiterte Auflage, Springer, Heidelberg, S. 11-45