Gegenstand der Graphentheorie ist die Untersuchung von Graphen, deren Eigenschaften und ihren Beziehungen zueinander. Viele anwendungsrelevante Fragen lassen sich in der Sprache der Graphentheorie formulieren, so dass Teile der Graphentheorie von großer Bedeutung in andere Disziplinen, wie z.B. den Wirtschaftswissenschaften, der Informatik, Bioinformatik oder auch der Chemie sind.
Graphen
Ein Graph G=( V,E) besteht aus einer Menge V von Ecken (vertices, Knoten) und einer Menge E von Kanten (edges, Linien) zusammen mit einer Inzidenzrelation, welche zu jeder Kante e zwei Ecken v,w assoziiert, die Enden der Kante e. Ist v=w, so nennt man e eine Schleife (loop), gibt es mehrere Kanten zwischen zwei Ecken v,w dann spricht man von einer Multikante. Die Enden einer Kante sind adjazent, und zwei Kanten mit einer gemeinsamen Ecke sind inzident. Der Eckengrad einer Ecke v ist die Anzahl der zu v inzidenten Kanten. Endliche Graphen haben eine endliche Ecken- und eine endliche Kantenmenge; andernfalls spricht man von unendlichen Graphen. Bei gerichteten Graphen haben die Kanten eine Richtung (die Kante wird dann durch einen Pfeil visualisiert). Gerichtete Graphen sind besonders interessant bei dem Studium von Flussproblemen.
Themen
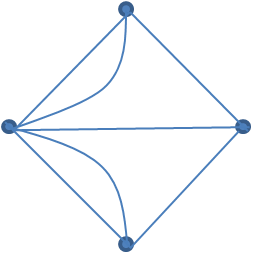
Die Anfänge der Graphentheorie gehen bis in das Jahr 1736 zurück, als Leonard Euler das Königsberger Brückenproblem formulierte und löste. Die Frage war, ob es einen Rundgang durch die Stadt Königsberg gibt, der jede der sieben Brücken über den Fluss Pregel genau einmal nutzt. Der nebenstehende Graph stellt das Problem dar. Euler bewies folgenden, für die Graphentheorie typischen Satz: Es gibt in einem Graphen G genau dann einen Rundweg, der jede Kante genau einmal durchläuft, wenn G zusammenhängend ist und jede Ecke einen geraden Eckengrad hat. Diese Fragestellung ist ein Spezialfall eines Optimierungsproblems mit vielfältigen Anwendungen in den Wirtschaftswissenschaften – dem Briefträgerproblem (Chinese Postman Problem): Gegeben ein Graph G und eine Gewichtsfunktion auf den Kanten. Gesucht wird ein Rundweg minimalen Gewichts, der jede Kante mindestens einmal durchläuft.
Analog lassen sich Fragen nach der Existenz von Rundwegen stellen, die jede Ecke genau einmal enthalten; solche Rundwege werden Hamiltonkreise genannt. Werden die Kanten gewichtet, so ist die Frage nach einem Hamiltonkreis mit minimalem Gewicht in G das Problem des Handlungsreisenden (Traveling Salesman Problem). Dieses, graphentheoretisch einfach zu formulierende Problem, hat eine Vielzahl von Anwendungen in der Industrie. Aufgrund seiner hohen Komplexität (NP-hart) wird in vielen Anwendungsfällen mit speziellen auf die Problemstellung zugeschnittenen Heuristiken gearbeitet, die Annäherungen an optimale Lösungen ermöglichen.
Ein Graph G=( V, E) ist bipartit, wenn seine Eckenmenge V aus zwei disjunkten unabhängigen Mengen A, B besteht und jede Kante zu einer Ecke aus A und zu einer aus B inzident ist. Viele Zuordnungsprobleme (z.B. Jobs auf Maschinen) lassen sich als Fragen nach Matchings (eine unabhängige Menge von Kanten) in bipartiten Graphen modellieren.
Ein die Graphentheorie stark beeinflussender Satz ist der Vierfabensatz, der sagt, dass die Ecken eines planaren Graphen mit vier Farben so gefärbt werden können, dass adjazente Ecken verschieden gefärbt sind. Die topologische Graphentheorie beschäftigt sich mit der Einbettbarkeit von Graphen in topologische Flächen, was auch Anwendungen z.B. im Chipdesign hat. Die Charakterisierung planarer Graphen durch verbotene Minoren kann als Anfangspunkt Entwicklung der Minorentheorie von Robertson, Seymour gesehen werden. Dies ist eine der weitreichensten und tiefsten Theorien in der Graphentheorie mit vielen, auch die Komplexität von Algorithmen betreffende Konsequenzen.
Strukturuntersuchungen durch Graphhomomorphismen stellen ein weiteres sehr aktives Forschungsgebiet der Graphentheorie dar. Einen hervorragenden Überblick über die Graphentheorie mit ihren Verbindungen zu anderen mathematischen Disziplinen und Anwendungsgebieten bieten die beiden Ausgaben des Handbook of Combinatorics.
Literatur
Diestel, Reinhard: Graphentheorie. 3. Auflage, Heidelberg: Springer-Verlag, 2006.
Graham, Ronald L.; Grötschel, M; Lovász, László (ed.): Handbook of Combinatorics.
Volume 1 ,2: Elsevier Science B.V., Amsterdam; MIT Press, Cambridge, MA, 1995.