Während für die effiziente Distribution von Gütern unter Einhaltung von Kundenzeitfenstern zahlreiche heuristische Verfahren exisitieren, gehören Berücksichtung von tageszeitabhängigen oder stochastischen Fahrzeiten, Ausnutzung von Umladungs- oder dynamischen Umplanungsmöglichkeiten sowie Gestaltung effizienter Marktmechnismen für die dezentrale Planung zu den aktuellen Herausforderungen. t
Als Grundproblem der Tourenplanung zählt das Traveling Salesman Problem (TSP) des Auffindens
eines kürzesten Hamiltonischen Zyklus in einem bewerteten Graphen – also der
kürzesten Rundreise – seit langem zu den meistuntersuchten diskreten
Optimierungsproblemen [Lawler et al. 1985]. Trotz NP-Vollständigkeit erlauben
Schnittebenen-Verfahren heute die optimale Lösung von Probleminstanzen mit
mehreren tausend Knoten.
Wichtige Generalisierungen und zusätzliche Nebenbedingungen
Sobald jedoch mehrere Fahrzeuge und zusätzliche
Nebenbedingungen wie z.B. Fahrzeugkapazitäten in Vehicle-Routing-Problemen
(VRP) zu berücksichtigen sind, muss auf heuristische Verfahren ausgewichen
werden. Naturanaloge Metaheuristiken wie Simulated Annealing, Genetische
Algorithmen, aber auch Tabu Search sowie Hybridverfahren unter Einbeziehung von
Constraint Propagation, kommen hierbei zur Anwendung [vgl. z.B. Pisinger/Ropke 2007].
Gleiches gilt für die Generalisierung des VRP zum Pickup-and-Delivery-Problem
(PDP), in welchem die Beladung der Fahrzeuge nicht nur in einem oder mehreren
dedizierten Depots stattfindet, sondern Aufträge prinzipiell von jedem
Netzwerkknoten (Origin) zu jedem anderen Netzwerkknoten (Destination) zulässig
sind.
Praxisrelevant sind insbesondere die Erweiterungen des VRP oder
PDP um Zeitfenster, die bei Origin und
Destination eingehalten werden müssen und entweder als harte Nebenbedingungen
modelliert oder bei Verfehlung über Strafkosten in die Zielfunktion einbezogen
werden. [vgl. z.B. Soumis et al. 1998]
Stochastische, dynamische und dezentrale Tourenplanung
Während das VRP auch mit stochastischer
Kundennachfrage bereits häufiger untersucht wurde [Gendreau et al. 1996], finden tageszeitabhängige und/oder stochastische Fahrzeiten
in der Tourenplanung erst in jüngerer Zeit nennenswerte Beachtung [vgl. Kenyon/Morton 2003], Hierbei wird meist eine
strikte Trennung von Planungszeitraum und Ausführungszeitraum des Plans unterstellt, was
mit zunehmender Verfügbarkeit mobiler IT immer weniger begründet werden kann,
sondern durch Möglichkeiten der Planung und Umplanung während der Ausführung
ergänzt werden muss.
Selten behandelt wurde bisher
das Problem der Transshipments, also die Beförderung
einzelner Aufträge mittels mehrerer Fahrzeuge mit Umladung [vgl. Mitrovic-Minic/Laporte 2006], wenngleich die Verwendung
von Distributionszentren in der Praxis fast den Regelfall darstellt.
Unterstellt man im Gegensatz zu den bisherigen Ausführungen keine
zentrale Planungsinstanz, sondern versteht die Annahme oder den Austausch von
Beförderungsaufträgen zwischen einzelnen Touren als marktlichen Prozess, so
zeigt sich schnell, dass sich die Komplexität des Problems nun in der
Schwierigkeit der Berechnung adäquater Gebots-Preise widerspiegelt: Die
Verbundeffekte erfordern kombinatorische Auktionen zur Lösung des Problems
einer pareto-optimalen Allokation, wie folgende Abbildung andeutet.
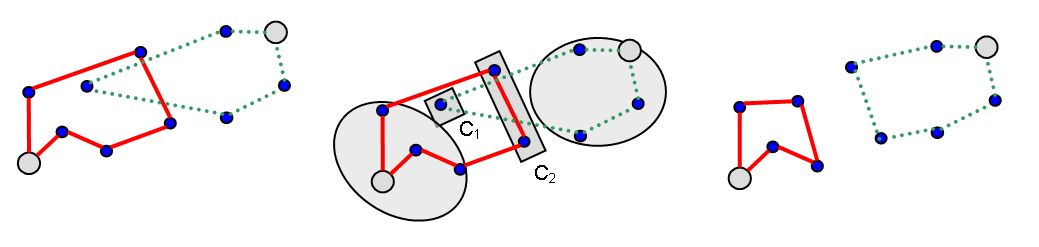
Abb. 1:
Komplementaritäten beim Austausch von Lieferaufträgen
Besteht z.B. eine
Kapazitätsgrenze oder Kundenzeitfenster, so kann der simultane Tausch von
Auftragscluster C1 und C2 zwischen den beiden Touren ggf. zu Einsparungen führen,
die durch sukzessive „Veräußerung“ einzelner Aufträge nicht realisierbar wären.
Wie diese Einsparungen anreizkompatibel unter den Marktteilnehmern aufgeteilt
werden können, stellt eine wesentliche Herausforderung für das sog. Mechnism
Design dar [vgl. Krajewska/Kopfer 2006].
Literatur
Gendreau,r Michel ; Laporte, Gilbert ; Seguin,r Rene: Stochastic vehicle routing. In: European Journal of Operational Researchr (1996), S. 3-12.
Kenyon,r Astrid S. ; Morton, David P.: Stochastic Vehicle Routing with Random Travelr Times. In: Transportation Science 37 (2003), Nr. 1, S. 69-82.
Krajewska,r Marta Anna ; Kopfer, Herbert: Collaborating freight forwarding enterprises. In:r OR Spectrum 28 (2006), Nr. 3, S. 301-436.
Lawler,r E.L. ; Lenstra, J.K. ; Rinnooy Kan, A.H.G. ; Shmoys, D.B. ; eds.: The travelingr salesman problem. A guided tour of combinatorial optimization. (Hrsg.): Wiley-Interscience series inr discrete mathematics. John Wiley & Sons (1985).
Mitrovic-Minic, Snezana ; Laporte, Gilbertr : The pickup and delivery problem with time windows and transshipment. INFOR 44 (2006), S.r 217-227.
Pisinger,r David ; Ropke, Stefan: A general heuristic for vehicle routing problems. In:r Computers & Operations Research 34 (2007), S. 2403-2435.
Soumis,r Francois ; Lavigne, June ; Desaulniers, Guy: Multi-depot vehicle schedulingr problems with time windows and waiting costs. In: European Journal ofr Operational Research 111 (1998), S. 479-494