Bei einem nichtlinearen Optimierungsmodell können die Restriktionen und/oder die Zielfunktion nicht durch lineare Funktionen ausgedrückt werden. Es gibt keinen allgemeinen Algorithmus, der in der Lage ist, für jedes nichtlineare Optimierungsmodell eine optimale Lösung zu bestimmen. Für spezielle Problemtypen sind Algorithmen entwickelt worden, die besondere Problemeigenschaften berücksichtigen.
Nichtlineare Optimierungsprobleme treten in der Praxis häufig auf. Beispiele sind das Transportkostenproblem mit mengenabhängigen Versandkosten, eine Depotzusammensetzung mit nicht festverzinslichen Wertpapieren oder die Verringerung der Stückkosten durch den Lerneffekt (d. h. effizientere Produktion durch größere Erfahrung).
Die Modellierung von nichtlinearen Zusammenhängen ist meistens sehr aufwendig. Oft können nichtlineare Probleme jedoch durch spezielle Modellierungstechniken linearisiert werden, so dass sie einer Standardsoftware zugänglich sind.
Quadratische Optimierung
Bei der quadratischen Optimierung sind die Restriktionen linear, aber die Zielfunktion wird als Summe von Termen ausgedrückt, die höchstens vom zweiten Grad sind. Zusätzlich zu linearen Termen sind nur Terme der Form k1x12oder k2x1x2 erlaubt, wobei x1 und x2 Entscheidungsvariablen sind. Solche Probleme entstehen bei der Portfolioanalyse und Standortplanung. Lösungsmethoden für die quadratische Optimierung sind in einigen Standardsoftwarepaketen enthalten, u.a. in IBM ILOG CPLEX und FICO XPRESS-Optimizer.
Separable Optimierung
Bei der separablen Optimierung können Zielfunktion und Restriktionen als Summe von Funktionen, die jeweils nur von einer Entscheidungsvariablen abhängen, ausgedrückt werden. Solche Modelle können durch eine stückweise lineare Zielfunktion approximiert und als gemischt-ganzzahlige Optimierungsmodelle gelöst werden (Abb. 1).
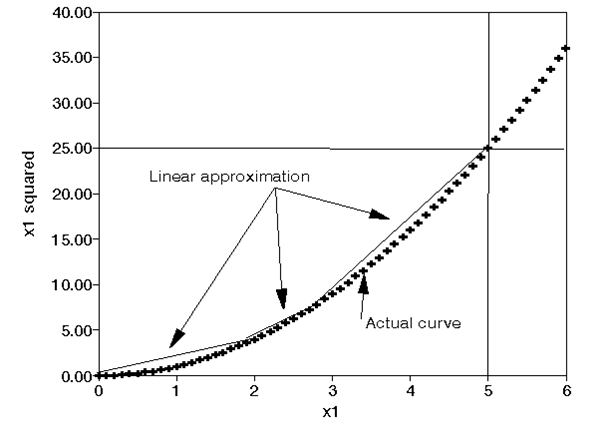
Abb. 1: Stückweise lineare Funktion
Eine stückweise lineare Zielfunktion entsteht oft im Rahmen von sprunghaften Rabatt- oder Preistafeln.
Allgemeine nichtlineare Optimierung
Unter bestimmten Bedingungen können nichtlineare Modelle mit iterativen Verfahren, z.B. Gradientenverfahren oder Newton-Verfahren approximativ gelöst werden. Eine Schwierigkeit dabei ist das Vermeiden von lokalen Optima, die nicht das globale Optimum darstellen. Wenn die Zielfunktion konkav (für ein Maximierungsproblem) oder konvex (für ein Minimierungsproblem) ist, können spezielle Methoden der konvexen Programmierung genutzt werden.
Allgemeine Solver für nichtlineare Modelle sind u.a. Conopt [Conopt 2011] und Minos [Minos 2011].
Literatur
Avriel, M.: Nonlinear Programming: Analysis and Methods. Dover Publishing 2003.
Bazaraa, M.S.; Sherali H.D.; Shetty, C.M.: Nonlinear Programming: Theory and Algorithms. 3rd edition, New York 2006.
Conopt http://www.conopt.com. Abruf am 31.08.2011.
Minos: http://www.sbsi-sol-optimize.com/asp/sol_products_minos_desc.htm. Abruf am 31.08.2011