Bei linearen Optimierungsmodellen (LP) sind Zielfunktion und Restriktionen lineare Funktionen der Entscheidungsvariablen. Jede Variable darf nur Werte in einem reellen Intervall [l,u] annehmen. Im Normalfall ist l = 0; einzelne l und u können auch – unendlich oder + unendlich sein.
Anwendungsgebiete
Lineare Optimierung kann grundsätzlich überall angewandt werden, wo knappe Ressourcen zur Verfügung stehen und eine lineare Zielfunktion maximiert werden soll, oder wo unter Einhaltung von linearen Restriktionen Kosten minimiert werden sollen. In der Praxis wird sie seit ca. 1960 eingesetzt, z.B. in Ölraffinerien sowie Prozess- inkl. Lebesmittelindustrie im Allgemeinen.
In der Praxis noch wichtiger als die reine lineare Optimierung mit kontinuierlichen Variablen ist die Lösung von LP-Modellen als Unterprobleme bei der gemischt-ganzzahligen Optimierung.
Modell und Lösungsverfahren
Jedes lineare Optimierungsmodell kann formal dargestellt werden als
min cx,
Ax <= b
l <= x <= u,
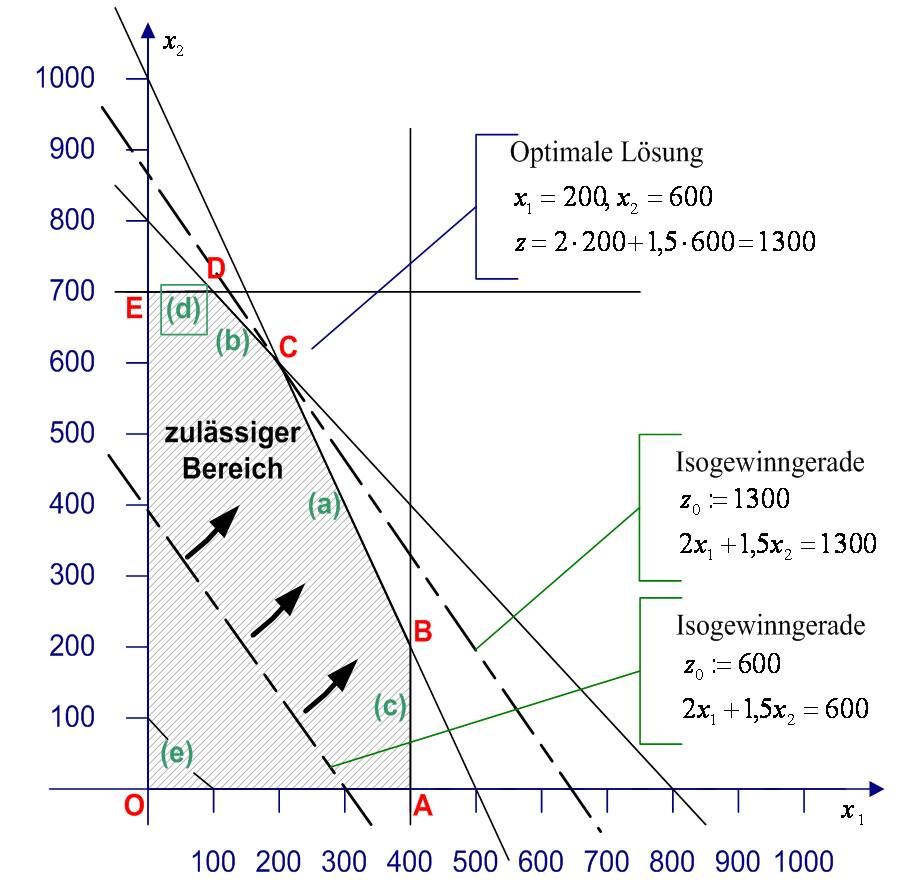
wobei x eine nx1-Vektor der Entscheidungsvariablen, c ein 1xn-Vektor der Zielfunktionskoeffizienten, A die Koeffizientenmatrix zur Darstellung der linearen Restriktionen und b die rechte Seite (beispielsweise zur Darstellung von Obergrenzen der Restriktionen) ist. Die nx1-Vektoren l und u stellen die Unter- und Obergrenzen der Variablen dar. Man kann beweisen, dass eine optimale LP-Lösung (wenn es eine gibt) sich an einem Eckpunkt des zulässigen Bereichs befindet. Abbildung 1 zeigt als ein einfaches Beispiel ein Modell mit einer optimalen Lösung im Punkt C).
|
|
Das Optimierungsmodell: max z = 2×1 + 1, 5×2 s.d. 2×1 + x2 ≤ 1000 x1 + x2 ≤ 800 x1 ≤ 400 x2 ≤ 700 x1, x2 ≥ 0 |
Abb. 1: Graphische Darstellung eines LP-Modells (rechts) mit zwei Variablen und zwei Restriktionen
Das älteste und bekannteste Lösungsverfahren für LP ist die (primale)
Simplex-Methode, die von George B. Dantzig im Jahr 1947 zur Lösung von Planungsproblemen bei der U. S. Air Force vorgestellt wurde [Dantzig 1959, Chvátal 1983]. Die duale Simplex-Methode ist eine wichtige Variante und konvergiert häufig schneller als das ursprüngliche primale Simplex-Verfahren.
Heutzutage immer wichtiger werden die aus der nichtlinearen Optimierung stammenden Innere-Punkte-Verfahren. Wo die iterativ berechneten Lösungen der Simplex-Methode sich auf der Oberfläche des zulässigen Bereichs bewegen, sind die Lösungen der Innere-Punkte-Verfahren im inneren Bereich dessen. Khachian zeigte 1979, dass mit der Ellipsoidmethode LP in polynomieller Zeit lösbar sind. In der Praxis haben sich jedoch die nicht-polynomiellen primal-duale Barrier-Methoden etabliert.
Beide Verfahrensklassen weisen unterschiedliche Vor- und Nachteile auf und ergänzen sich.
Die Stärke der linearen und gemischt-ganzzahligen Optimierung beruht vor allem darauf, dass es hoch entwickelte Standardsoftware gibt, die in der Lage ist, viele der praxisrelevanten Modelle zu lösen. Die State-of-the-Art-Solver sind durch unzählige Verbesserungsschritte weiter ausgereift worden. Wo die Lösung eines typischen Benchmark-Modells im Jahr 1990 in 612 Sekunden gelöst wurde, dauerte die Lösung 2011 nur noch 0,6 Sekunden ( [MOPS 2011], s. auch [Bixby 2002]). Der Fortschritt ist in etwa gleichen Anteilen auf Hardwareverbesserungen und algorithmische Entwicklungen zurückzuführen.
Weil auch sehr große LP-Modelle heute optimal gelöst werden können, tendiert man in praktischen Anwendungen zu immer größeren Modellen. Viele der größten heute gelösten Modelle stammen aus dem Bereich Logistik und Transport, z.B. beinhalten Besatzungseinsatzprobleme großer Fluggesellschaften bis zu 12 Millionen Variablen.
Leistungsfähige kommerzielle LP-Solver sind ILOG CPLEX
(s. http://www.ilog.com/products/cplex/), XPRESS-MP (s. http://www.dashoptimization.com/) und MOPS (s. http://www.mops-optimizer.com/). Bekannte Open-Source-Codes sind COIN-OR (http://www.coin-or.org) und GLPK (http://gnu.org/software/glpk).
Literatur
Bixby, R. E.: Solving real-world linear programs: a decade and more ofr progress. Operations Research 50 (2002), Nr. 1, S. 3-15.
Chvátal, V.: Linear Programming. W. H. Freeman 1983.
Dantzig, G.: Linear Programming and Extensions. Princeton : Princeton University Press 1959.
Maros, I.: Computational Techniquesr of the Simplex Method, Kluwer’s International Series, 2003
MOPS Optimierungssysteme: MOPS White Paper. S. http://www.mops-optimizer.com, Abruf 31.08.2011